
, in which you add up a finite number of terms. The terms becomes too large, as with the geometric growth, if \(|r| > 1\) the terms in the sequence will become extremely large and will converge to infinity.
#Sum of geometric sequence converge series
\Īn important result is that the above series converges if and only if \(|r| 1\) \), and will add these terms up, like:īut since it can be tedious to have to write the expression above to make it clear that we are summing an infinite number of terms, we use notation, as always in Math. In other words, we have an infinite set of numbers, say \(a_1, a_2. It does not have to be complicated when we understand what we mean by a series.Īn infinite series is nothing but an infinite sum. Thereforethe geometric series converges precisely when jrj<1 and diverges. (If r 1 and a 6 0, then lim N1 S N lim N1 aN 1 ).
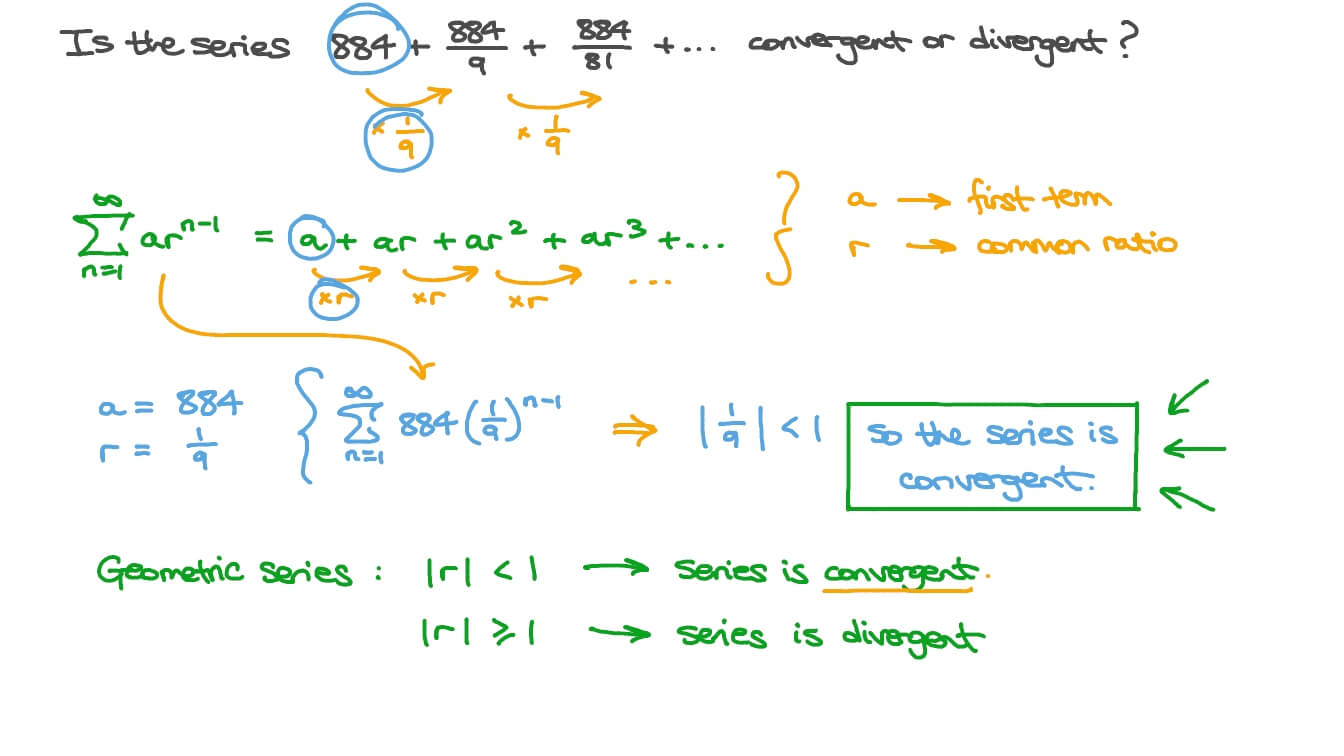
The concepts in this exercise show up in second semester calculus as related to Taylor polynomials.Summation (or sigma) notation is a notation used for representing long sums.If the common ratio is -1, the series will tend to oscillate, and it diverges to infinity if the magnitude of the ratio is greater than one.

It only converges if the magnitude of the ratio is less than one. The infinite geometric series is the limit as n goes to infinity of the finite geometric series formula.Because both of these series converge we can break it into the difference of two series to sum it. The infinite geometric series formula is S ∞ = g 1 1 − r. If r 1, the geometric series is divergent.Knowledge of geometric sequences and beginning ideas of convergence are encouraged to ensure success on this exercise. The user is asked to determine which function is being represented by the sum. Find the function representation: This problem provides an infinite geometric series that can be written as a continuous function in x.The user is asked to select all of the series that converge from the multiple select list. Evaluate sigma notation: This problem also has the user find an infinite geometric sum, this time, written in the sigma notation.Įvaluate sigma notation Determine convergence: This problem provides several geometric series.The user is asked to solve the problem and provide the correct answer. Solve the word problem: This problem provides a real-life application that involves an infinite geometric sum.Once a common factor is removed from the series, you end up with a value raised to a series of consecutive powers. What is a Geometric Series A geometric series (or geometric progression) is one where every two successive terms have the same ratio. The user is tasked with finding some other piece of missing information based on the givens. Sum of a Convergent Geometric Series Rth Moment Related article: Finite Geometric sequences. Given the sum, find other information: This problem provides the sum of an infinite geometric sequence and some other information.The user is expected to find the correct answer and write it in the space provided. If the sequence of partial sums of the series does not converge, we say that the series diverges. In this case we write X n1 a n a1 +a2 +a3 ++a n + L. Find the sum: This problem provides an infinite sum. If the sequence of partial sums converges to a limit L, we say that the series converges and that the sum is L.In this case we write X n1 a n a1 +a2 +a3 +··

There are six types of problems in this exercise: If the sequence of partial sums converges to a limit L, we say that the series converges and that the sum is L. This exercise uses a plethora of problems to explore the sum of infinite geometric sequences. The Infinite geometric series exercise appears under the Precalculus Math Mission, Mathematics III Math Mission and Integral calculus Math Mission.


 0 kommentar(er)
0 kommentar(er)
